Chào mừng bạn đến với series Dopex Essentials giúp mọi người làm quen với những kiến thức cơ bản về giao dịch quyền chọn. Mọi người nên bắt đầu với từ phần đầu tiên của series để nắm được những kiến thức xuyên suốt.
Trong phần này, chúng ta sẽ tìm hiểu sâu về Option Gamma. Có khá nhiều vấn đề liên quan đến tính toán và một số khái niệm khó nắm bắt nên bài viết sẽ trình bày một cách đơn giản nhất về Option Gamma.
Đây là danh sách trọn bộ các phần của Series này:
Ngoài series này, mọi người cũng có thể tham khảo thêm những bài viết sau để có thể hiểu hơn về Option Trading và Dopex nhé!
Có một bảng chú thích cho các thuật ngữ ở cuối bài viết, vì vậy nếu bạn đọc đến những thuật ngữ lạ, hãy lướt xuống phía dưới để tham khảo!
Gamma là gì?
Gamma của một quyền chọn đo lường khả năng biến thiên của giá trị Delta theo sự thay đổi về giá của tài sản cơ sở. Gamma giúp chúng ta trả lời câu hỏi này - “Ứng với một sự thay đổi nhất định về giá của tài sản cơ sở thì Delta của quyền chọn sẽ thay đổi như thế nào?”
Trước khi đi sâu hơn vào bài viết, chúng ta có thể liên tưởng một vài điểm tương đồng giữa Delta và Gamma với vận tốc và gia tốc của một chất điểm.
Nhớ Về Lí Thuyết Vận tốc

Vận tốc là tốc độ thay đổi khoảng cách (được tính bằng sự thay đổi quãng đường chia cho thời gian chuyển động). Về mặt giải tích, vận tốc là đạo hàm bậc nhất của quãng đường đã đi.
Gia tốc
Gia tốc là tốc độ thay đổi của vận tốc (tức là sự thay đổi của vận tốc theo thời gian). Về mặt giải tích, có thể coi gia tốc là đạo hàm bậc hai của quãng đường đã đi hoặc đạo hàm bậc nhất của vận tốc.
Đạo hàm bậc nhất
Tương tự về mặt quyền chọn, sự thay đổi trong giá của quyền chọn (hay phí premium) dựa trên sự thay đổi giá của tài sản cơ bản là một giá trị có thể định lượng được và gọi là Delta. Vậy Delta chính là đạo hàm bậc nhất của phí premium.
Đạo hàm bậc hai
Biến thiên giá trị của Delta theo sự thay đổi về giá của tài sản cơ sở là một giá trị gọi là Gamma. Tương tự như cách hiểu về gia tốc, Gamma là đạo hàm bậc hai của phí premium, và cũng là đạo hàm bậc nhất của Delta.
Chắc rằng bạn đọc có thể ngại về việc tính toán các giá trị Delta và Gamma cho quyền chọn phải đòi hỏi đụng chạm đến rất các phép tính phức tạp (như là các phương trình vi phân). Đừng lo vì bài viết này sẽ không đào sâu vào chuyện đó.
Funfact: Derivatives vừa có nghĩa là các công cụ tài chính phái sinh, cũng vừa có nghĩa là "đạo hàm". Giá trị mà các hợp đồng tương lai và quyền chọn phái sinh được tính toán bằng cách sử dụng "đạo hàm" như một khái niệm toán học. Vì vậy các hợp đồng tương lai và quyền chọn được gọi là "Derivatives".
Tiếp tục…
Chúng ta đã chứng minh nhiều lần rằng Delta của một quyền chọn có thể liên tục thay đổi giá trị tương ứng với sự thay đổi giá của tài sản cơ sở. Cùng nhìn lại biểu đồ Delta vs Spot Price được đề cập trong bài viết trước.
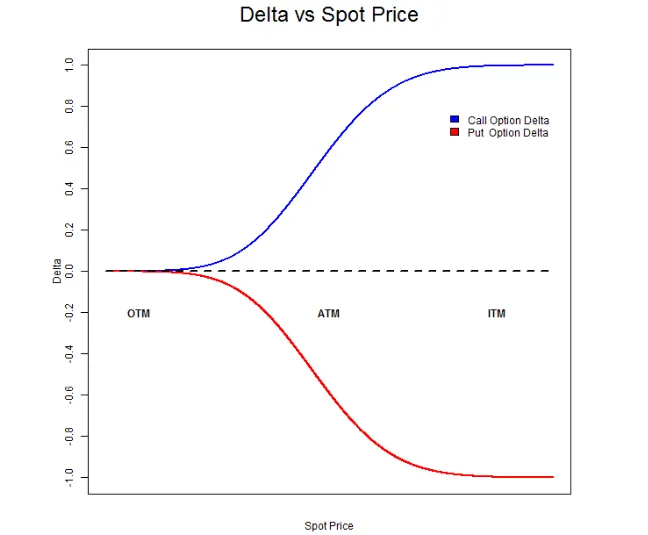
Như có thể thấy qua biểu đồ trên, Delta thay đổi theo giá của tài sản cơ sở. Câu hỏi đặt ra là:
- Tại sao sự thay đổi của giá trị Delta lại quan trọng?
- Làm thế nào chúng ta có thể ước tính chính xác sự thay đổi của giá trị Delta?
Chúng ta sẽ giải quyết câu hỏi thứ hai trước tiên:
Như đã đề cập ở trên, Gamma được tính bằng đạo hàm của phí Premium trong quyền chọn. Gamma được tính bằng sự thay đổi của giá trị Delta trên mỗi thay đổi nhỏ nhất ($1) của giá tài sản cơ sở. Delta tăng một lượng bằng đúng giá trị Gamma khi giá tài sản tăng $1, và ngược lại, Delta giảm một lượng bằng đúng giá trị Gamma khi giá tài sản cơ sở giảm $1.
Đến với ví dụ đầu tiên:
nhãn | giá trị |
|---|---|
Giá HakkoToken | $8,326 |
Giá thực hiện | $8,400 |
Kiểu option | Call option |
Moneyness of Option | Slightly OTM |
Giá của quyền chọn (phí premium) | $26 |
Delta | 0.3 |
Gamma | 0.0025 |
Giá tài sản sở tăng | $70 |
Giá mới của tài sản cơ sở | 8,326 + 70 = $8,396 |
Giá mới của quyền chọn | ? |
Delta mới | ? |
Gamma mới | ? |
Tính toán
nhãn | giá trị |
|---|---|
Giá quyền chọn thay đổi | Delta x Sự thay đổi của giá tài sản cơ sở 0.3 x 70 = $21 |
Giá mới của quyền chọn | 21 + 21 = $47 |
Tỉ lệ thay đổi của Delta (Gamma) | 0.0025 (Delta tăng 0.0025 khi giá tăng $1) |
Mức tăng của Delta | Gamma x Sự thay đổi của giá tài sản cơ sở 0.0025 x 70 = 0.175 |
Giá của quyền chọn (phí premium) | $26 |
Delta mới | Delta cũ + lượng thay đổi 0.3 + 0.175 = 0.475 |
Trạng thái moneyness mới của quyền chọn | (Slightly OTM ->) ATM |
Rõ ràng, khi giá của HakhoToken chuyển từ $8.326 lên $8.396, giá của quyền chọn đã thay đổi từ $26 lên $47 và Delta của quyền chọn thay đổi từ 0.3 thành 0.475.
Với sự thay đổi 70 điểm, Tính moneyness của quyền chọn sẽ chuyển từ Slightly OTM sang ATM. Về mặt lý thuyết, điều đó có nghĩa là Delta của quyền chọn phải thay đổi từ 0.3 thành một giá trị gần với 0.5. Đó là những gì xảy ra trong ví dụ trên.
Ví dụ thứ hai:
Lần này giả sử HakhoToken tăng thêm $70 nữa từ $8.396 lên $8.466. Điều gì sẽ xảy ra với quyền chọn mua $8.400 (Từ giờ sẽ gọi là quyền chọn Y) của chúng ta ?
nhãn | giá trị |
|---|---|
Giá trước đó của tài sản cơ sở | $8,396 |
Giá mới tài sản cơ sở | $8,396 + $70 = $8,466 |
Giá trước đó của quyền chọn | $47 |
Delta trước đó của quyền chọn | 0.475 |
Thay đổi trong giá của quyền chọn | 0.475 x 70 = $33.25 |
Giá mới của quyền chọn | $47 + $33.25 = $80.25 |
Trạng thái moneyness mới của quyền chọn | (ATM ->) ITM |
Thay đổi trong giá trị Delta | 0.0025 x 70 = 0.175 |
Delta mới | 0.475 + 0.175 = 0.65 |
Ví dụ thứ ba:
Giả sử HakhoToken giảm $50, điều gì sẽ xảy ra với quyền chọn Y? Hãy làm rõ từng biến chuyển:
nhãn | giá trị |
|---|---|
Giá trước đó của tài sản cơ sở | $8,466 |
Giá mới tài sản cơ sở | $8,396 - $50 = $8,416 |
Giá trước đó của quyền chọn | $80.25 |
Delta trước đó của quyền chọn | 0.65 |
Thay đổi trong giá của quyền chọn | 0.65 x (-50) = -$33.25 |
Giá mới của quyền chọn | $80.25 - $33.25 = $47.75 |
Trạng thái moneyness mới của quyền chọn | (ITM ->) Slightly ITM |
Thay đổi trong giá trị Delta | 0.0025 x (-50) = -0.125 |
Delta mới | 0.65 - 0.125 = 0.525 |
Speed (Gamma của Gamma)
Bạn có thể thắc mắc tại sao giá trị Gamma lại không đổi trong các ví dụ trên đây trong khi trên thực tế, giá trị của Gamma cũng thay đổi cùng với sự thay đổi về giá của tài sản cơ sở.
Sự biến thiên của giá trị Gamma do những thay đổi về giá của tài sản cơ sở được tính bằng đạo hàm bậc ba của Premium, được gọi là “Speed” hoặc “Gamma của Gamma” hoặc “sự thay đổi của Gamma chia cho sự thay đổi về giá của tài sản cơ sở”. Tuy nhiên, chúng ta sẽ không đi sâu vào vấn đề đó ngay bây giờ.
Tiếp tục, như bạn có thể nhận thấy, không giống như giá trị Delta, Gamma LUÔN là số dương, đối với cả quyền chọn mua và quyền chọn bán.
Bạn có thể đã nghe các nhà giao dịch sử dụng thuật ngữ “Long Gamma”, điều này đơn giản có nghĩa là nhà giao dịch đang mua cả quyền chọn mua và quyền chọn bán. Hoặc ngược lại, nhà giao dịch có thể sử dụng thuật ngữ 'Short Gamma” khi họ bán cả quyền chọn mua và quyền chọn bán.
Một vài ví dụ:
Câu hỏi cho bạn: Gamma của quyền chọn bán ATM (gọi là Quyền chọn A) là 0.004. Nếu giá của tài sản cơ sở thay đổi $10, bạn nghĩ Delta mới là bao nhiêu?
Trước hết chúng ta hãy nhớ lại rằng đối với quyền chọn ATM, độ lớn của Delta là 0.5 và đối với quyền chọn bán, giá trị Delta luôn âm. Do đó, giá trị Delta của quyền chọn A là -0.5. Chúng tôi đã xác định rằng Gamma luôn là số dương bất kể là quyền chọn gì. Dữ liệu từ câu hỏi cho biết giá tài sản cơ sở thay đổi $10, nhưng nó không cho biết hướng thay đổi, vì vậy chúng ta hãy xem xét cả hai kịch bản (tăng giá và giảm giá).
Trường hợp Alpha
Giá của tài sản cơ sở TĂNG $10
nhãn | giá trị |
|---|---|
Delta | -0.5 |
Gamma | 0.004 |
Giá tài sản cơ sở tăng | $10 |
Delta tăng | Gamma x Sự thay đổi của giá tài sản cơ sở 0.004 x 10 = 0.004 |
Delta mới | Độ lớn Delta của quyền chọn bán giảm khi giá của tài sản cơ sở tăng, vì vậy: -0.5 + 0.04 = -0.46 |
Trường hợp Alpha
Giá của tài sản cơ sở GIẢM $10
nhãn | giá trị |
|---|---|
Delta | -0.5 |
Gamma | 0.004 |
Giá tài sản cơ sở tăng | $10 |
Delta tăng | Gamma x Sự thay đổi của giá tài sản cơ sở 0.004 x (-10) = -0.004 |
Delta mới | Độ lớn Delta của quyền chọn bán tăng khi giá của tài sản cơ sở giảm, vì vậy: -0.5 + (- 0.04) = -0.54 |
Bảng chú giải thuật ngữ về Option
Tài sản cơ sở — Hợp đồng quyền chọn đang dự đoán giá của tài sản này, chẳng hạn như Bitcoin.
Ngày đáo hạn — Ngày quyền chọn sẽ đáo hạn và được thực hiện, sau ngày này, hợp đồng không còn hiệu lực.
Giá thực hiện - Giá mà người mua có quyền mua hoặc bán tài sản cơ sở khi đáo hạn.
Giá quyền chọn (premium) — Giá mà người mua trả cho người bán để có quyền mua hoặc bán tài sản theo giá thực hiện vào ngày đáo hạn.
In the money (ITM):
- Đối với quyền chọn mua - thuật ngữ này được sử dụng khi giá thực hiện thấp hơn giá trị thị trường của tài sản cơ sở.
- Đối với quyền chọn bán - thuật ngữ này được sử dụng khi giá thực hiện cao hơn giá trị thị trường của tài sản cơ sở.
At the money (ATM):
- Đối với cả quyền chọn mua và quyền chọn bán - thuật ngữ này được sử dụng khi giá thực hiện bằng với giá trị thị trường của tài sản cơ sở.
Out of the money (OTM):
- Đối với lệnh call option - thuật ngữ này được sử dụng khi giá thực hiện cao hơn giá trị thị trường của tài sản cơ sở.
- Đối với lệnh put option - thuật ngữ này được sử dụng khi giá thực hiện thấp hơn giá trị thị trường của tài sản cơ sở.
Tất cả các quyền chọn trên Dopex đều theo phong cách Châu Âu, có nghĩa là chúng chỉ có thể được thực hiện khi đáo hạn, không giống như các quyền chọn kiểu Mỹ có thể được thực hiện bất kỳ lúc nào cho đến khi đáo hạn hạn.
Giới thiệu về Dopex (Decentralized Option Exchange)
Dopex là một giao thức option trading phi tập trung nhằm mục đích tối đa hóa tính thanh khoản, giảm thiểu tổn thất cho người viết quyền chọn và tối đa hóa lợi nhuận cho người giao dịch option một cách thụ động.
Bài viết này được thực hiện dựa trên sự kết hợp giữa Dopex & Hak Research
💁 Disclaimer: Tất cả bài viết của Hak Research được cung cấp với mục tiêu là chia sẻ kiến thức và không được xem là lời khuyên đầu tư.
- BHO Network Chính Thức Phi Tập Trung Hoàn Toàn - November 19, 2024
- Copin.io: Khám Phá Insight Từ Perpetual DEX - October 30, 2024
- Counter Fire Tournament: Giải Đấu Game Web3 Hấp Dẫn Với Tổng Giải Thưởng Lên Đến 12,000 USDC - October 27, 2024







