Trong bài viết này, chúng ta sẽ thảo luận ngắn gọn, đơn giản hóa nhất có thể về những khái niệm như Black-Scholes Formula, Volatility Surfaces và Volatility Smiles. Bài viết sẽ tập trung vào ý nghĩa của các thuật ngữ này đối với giao dịch quyền chọn trên Dopex.

Trước khi tiếp tục, hãy nhớ đọc bài viết đầu tiên trong series này vì có những thuật ngữ mà bạn có thể không biết nhưng đã được giải thích trong bài viết trước. Đây là danh sách trọn bộ các phần của Series này:

Ngoài ra, mọi người cũng có thể tham khảo thêm những bài viết sau để có thể hiểu hơn về Option Trading và Dopex nhé!

Mô hình Black-Scholes

Mô hình Black-Scholes

Mô hình Black-Scholes là gì?

Black-Scholes là một mô hình toán học được xây dựng để định giá hợp đồng quyền chọn trên phương diện lý thuyết. Mô hình Black-Scholes sử dụng sự biến động của một quyền chọn làm giá trị đầu vào để định giá quyền chọn đó. 

Trong đó, mức độ biến động dự kiến của quyền chọn (thường được gọi là Implied Volatility hay Option Volatility) được hiểu là mức độ biến động dự kiến của giá tài sản cơ sở của quyền chọn đó trong tương lai. Độ biến động dự kiến càng lớn tức là thị trường đang cho rằng giá tài sản càng có khả năng tăng hay giảm nhiều.

Bộ Giả  Định Black-Scholes

Bộ giả định Black-Scholes là 6 điều kiện bắt buộc phải thỏa mãn để mô hình Black-Scholes có ý nghĩa. Xét trong trường hợp định giá hợp đồng quyền chọn với tài sản cơ sở là một cổ phiếu thì 6 điều kiện đó là:

1. Holder của cổ phiếu đang đề cập không được không được trả cổ tức
2. Quyền chọn được thực hiện là loại quyền chọn kiểu Âu
3. Thị trường tài chính luôn luôn hiệu quả (Có nghĩa là thông tin mới được phản ánh nhanh chóng và đầy đủ trong giá của tài sản, và do đó, việc cố gắng dự đoán sự biến động giá để kiếm lợi nhuận là khó khăn)
4. Tất cả các giao dịch không được ủy quyền
5. Lãi suất không đổi
6. Lợi nhuận của cổ phiếu cơ sở được phân phối chuẩn logarit

Mô hình Black Scholes cho rằng độ biến động của một quyền chọn là không đổi. Nhưng trên thực tế, nó luôn thay đổi. Do đó, giá (premium fee) của những quyền chọn có cùng mức giá thực hiện và thời điểm đáo hạn thường không giống với với giá lý thuyết là kết quả được tính bởi mô hình Black Scholes. 

Tóm lại, độ biến động của một quyền chọn là có thay đổi, và phụ thuộc vào hai yếu tố là (1) mức giá thực hiện và (2) thời hạn hợp đồng. Vì vậy có thể mô phỏng sự phụ thuộc của độ biến động dự vào hai biến trên thành một biểu đồ ba chiều có tên là Volatility Surfaces.

Volatility Surfaces

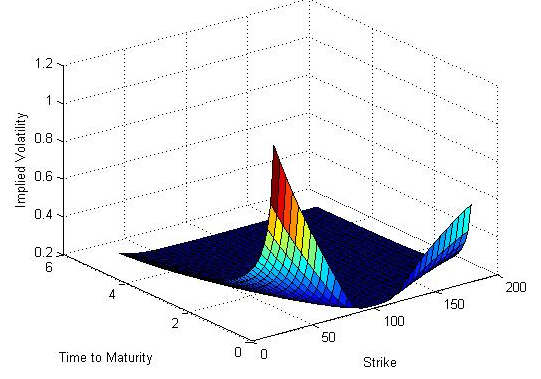
Volatility Surfaces là gì?

Volatility Surfaces là một đồ thị trong không gian ba chiều thể hiện mức độ biến động dự kiến (Implied volatility) dựa trên từng giá trị của giá thực hiện (Strike) và thời hạn hợp đồng (Time to Maturity). 

Giả sử mô hình Black-Scholes là hoàn toàn chính xác (Implied Volatility không đổi) thì Volatility Surfaces phải là một mặt phẳng. Tuy nhiên, thực tế không phải vậy, Volatility Surfaces không bằng phẳng và thay vào đó có xu hướng thay đổi theo thời gian (do trong điều kiện thị trường thực tế thì 6 điều kiện của mô hình Black Scholes không phải lúc nào cũng thỏa mãn).

Thời hạn hợp đồng (hay thời gian còn lại cho tới ngày đáo hạn của hợp đồng) càng lớn thì độ biến động dự kiến càng thấp. Các quyền chọn có thời hạn hợp đồng ngắn hơn thì càng có độ biến động cao hơn đáng kể.

Ứng với mỗi mức giá thực hiện nhất định nào, Implied volatility có thể tăng hoặc giảm theo thời gian cho đến khi đáo hạn, dẫn đến hiện tượng được gọi là Volatility Smiles.

Volatility Smiles

Khi moneyness (tương quan giá thực hiện và giá của tài sản cơ sở) càng OTM hoặc ITM (và cách càng xa trạng thái ATM) thì Implied volatility sẽ càng tăng lên.

Volatility Smiles là gì?

Volatility Smiles là hình dạng của một biểu đồ, thể hiện sự phụ thuộc của độ biến động dự kiến vào giá thực hiện. Cụ thể đồ thị thể hiện giá trị của độ biến động dự kiến theo giá thực hiện là một hình chữ U giống một nụ cười nên gọi đây là volatility smile.

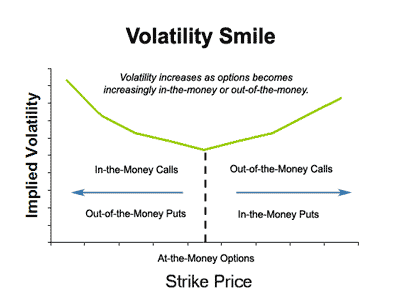
Mô hình Black-Scholes không dự đoán được Volatility Smiles. Như đã đề cập trước đó, Black-Scholes giả định rằng rằng khi vẽ biểu đồ dựa trên các mức giá thực hiện khác nhau, Implied volatility sẽ là một đường thẳng song song trục hoành. Nói cách khác, đối với các quyền chọn có cùng thời hạn hợp đồng, cùng tài sản cơ sở thì đều có cùng mức độ biến động dự kiến mà không phụ thuộc vào mức giá thực hiện.

Tuy nhiên, Mô hình Black-Scholes chỉ là lý thuyết. Trong thực tế, thị trường luôn có những sự kiện gây ra biến động mạnh. Khi những sự kiện này diễn ra, giá của tài sản cơ sở thay đổi và khả năng biến động của giá cũng tăng lên. Trong khi giá của tài sản cơ sở ảnh hưởng trực tiếp đến moneyness của quyền chọn. Vậy nên khi quyền chọn càng ITM hay OTM, biến động dự kiến cũng càng cao.

Công thức định giá Dopex AMM

Giao thức Dopex có một số chức năng linh hoạt trong việc cung cấp thanh khoản, lấy ý tưởng từ các nền tảng option sử dụng AMM thành công như Deribit và Robinhood.

Dopex AMM sử dụng tài sản từ những pool tài sản với cách tính giá của mô hình Black-Scholes, tính toán volatility smiles để cho phép người dùng mua quyền chọn dựa trên mức giá thực hiện và thời điểm đáo hạn trong tương lai. 

Chi phí để mua quyền chọn cũng được tính toán on-chain dựa trên mô hình Black-Scholes — sử dụng Implied volatility và giá tài sản được cung cấp bởi Chainlink — và chuyển qua một hàm để tính volatility smiles dựa trên mức độ biến động thực tế của tài sản và dữ liệu trong quá khứ.

Vấn đề trước mắt

Giá trị Implied volatility là không khách quan nếu không có dữ liệu từ sổ lệnh hoặc nếu thị trường quyền chọn của tài sản cơ sở vốn đã rất kém thanh khoản. Hiện tại, rất khó để định giá quyền chọn cho những tài sản kém thanh khoản trên thị trường quyền chọn như BTC và ETH.

Dopex giải quyết nó như thế nào

Mô hình định giá của Dopex là một hệ thống đồng thuận phi tập trung, được vận hành bởi nhiều đơn vị độc lập, mỗi đơn vị sẽ cung cấp các hệ số khác nhau để tính toán ra một volatility surfaces chung duy nhất, với điều kiện các đơn vị đó sẽ không công khai phương pháp tính hệ số của mình (để đảm bảo tính khách quan).

Giới thiệu về Dopex

Dopex là một giao thức quyền chọn phi tập trung nhằm mục đích tối đa hóa tính thanh khoản, giảm thiểu tổn thất cho người viết quyền chọn và tối đa hóa lợi nhuận cho người mua quyền chọn một cách thụ động.

Bài viết này được thực hiện dựa trên sự kết hợp giữa Dopex & Hak Research